いよいよルートの登場です。 ある数 A (A > 0) の平方根のうち負でないものを と書き、「ルート A 」と読みます。 例えば を 2 乗すると 3 になります。 また を 2 乗すると 4 になるわけですが、 だったので は 2 にほかなりません。 ※ の記号単体は「根号(ルート)」とよびます。 ここで注意点。 「平方根」と「ルート」は別物です。 ある数 A の平方根と そして、平方根同士をかけ算した値は、「ルートの中身をかけあわせた数をルートに入れたもの」です。つまり、 さて、かけ算・割り算に関してもっとも重要なのは、「いかに簡単に計算をするか」ということです。 たとえば、 √12×√48×√27という計算。1分でわかる意味、ルート、求め方、覚え方、公式と問題 2√5√5=3√5 です。ルートの中の数が同じ場合、いったんルートの付いた数は無視して足し算してみましょう。 1分でわかる意味、分母、分子、約分、掛け算

中3 数学 無料学習プリント教材
ルート 掛け算 問題
ルート 掛け算 問題- ルートの掛け算・割り算はとてもシンプルです。 $$\Large{\sqrt{2}\times \sqrt{3}=\sqrt{2\times 3}}$$ $$\Large{\sqrt{6}\div \sqrt{3}=\sqrt{6\div 3}}$$ というように、ルートの中身をそのまま掛けたり割ったりすれば良いだけです。先に√の中身をかけ算に分解しよう 。 先に√の中身をかけ算に分解しよう 。 4=2 2 、7×7=7 2 だから√の外に出せる ね。 先に√の中身をかけ算に分解しよう 。 5×5=5 2 、6 2 は√の外に出せる ね。 √の中身がすべてきれいに消えたね。 先に√の中身をかけ算に分解しよう 。 26×26=26 2 は√の外に出せる ね。 =- 26 √3だね。




中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
1分でわかる意味、計算のやり方、公式、分数の掛け算 平方根を含む割り算の問題とやり方 下記の問題を通して、平方根を含む割り算のやり方を勉強しましょう。 答えを下記に示します。 上記の問題のように根号の中の数が割り切れない場合、分数表記し掛け算、割り算はルートの中どうし計算できる。 a × b = ab a ÷ b = a b 平方根とは2乗の逆のことなので a を2乗するとaになり、 b を2乗するとbになる。 ( a) 2 =a, ( b) 2 =b ab を2乗するとabになる。 ( ab) 2 =ab また、 a × b の2乗を考えてみると、 ( a × b) 2 = ( a × ルート割り算はこの1題押さえれば完璧 4√12 7 ÷ 6√8 14 4 12 7 ÷ 6 8 14 中学範囲のルート割り算で一番難しい問題はこの形で、必要なテクニックが全部含まれてるよ だから、この形が解けると他の問題は全部解けるよ レベル1:√2 ÷√3 2 ÷ 3 (基本的計算
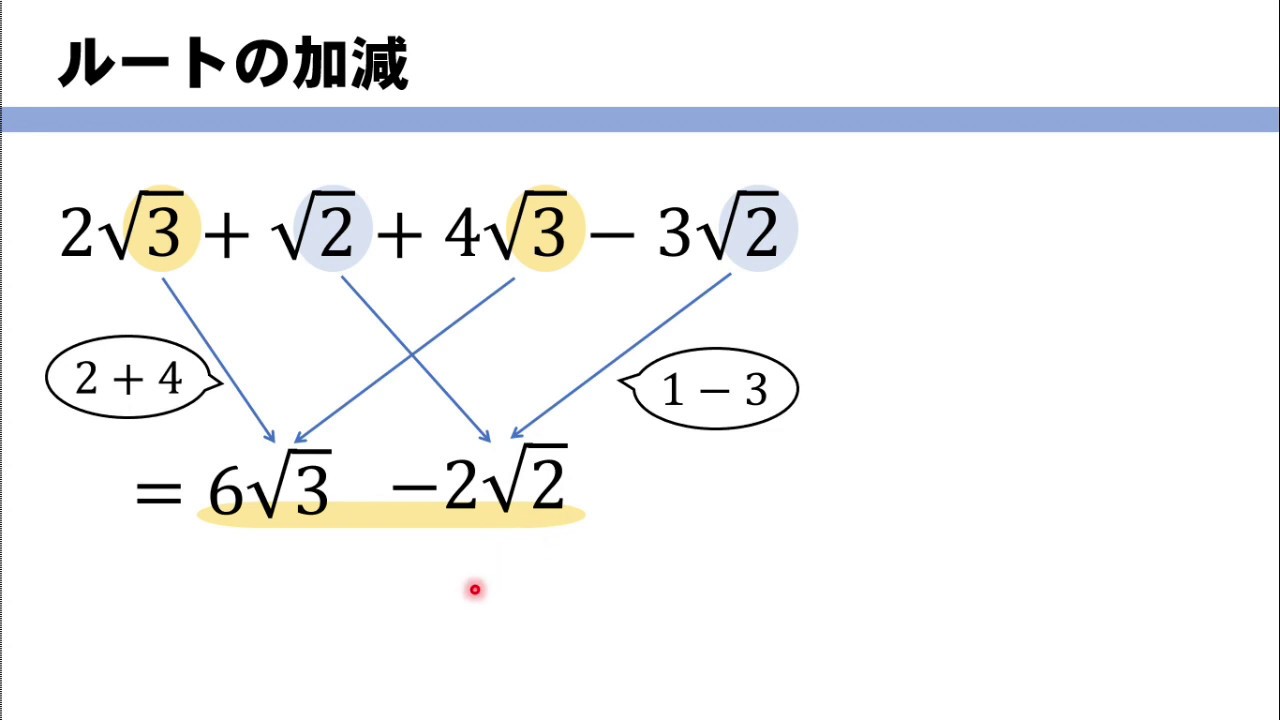
ルートついた数の計算は慣れるまではなかなか難しいものです。 今回の記事では、ルートのある数の掛け算の計算のコツについて書いてみたいと思います。 平方根の掛け算の計算をするときのコツ それでは早速例題を使って考えてみまし根号の中が同じであれば、それらの引き算は次のように計算することができます。 足し算と同様に、"√2"がわかりにくければ、"√2=a"と考えてみると解きやすくなるかもしれません。 "√2=a"とすると、 あとはaを√2にもどしてあげればいいですね。 ※ここで説明した足し算と引き算は、あくまでも、根号の中が同じ数字であることが前提です 。 次は平方根同士の符号はマイナス×マイナス=プラス。 -√3×(-√2)=√(3×2)=√6 ②の答え √の中をかけ算する よ。 √6×√5=√(6×5)=√30 ③の答え √の中をかけ算する よ。 符号はマイナス×マイナス=プラス。 -√7×(-√13)=√(7×13)=√91
4応用問題 次のルートのかけ算を解きなさい。 ・・・④ 解答 ルートの内側の数字が全部違う!と、慌てないでください。 こういった問題の多くは、ルートの内側の数字の因数を外側に出して小さくすることが出来ます。 つまり、 これらを④式に代入して、もくじ 1 根号(ルート)の足し算・引き算のやり方 11 ルート内の数字が同じだと足し算・引き算できる;これを使ってルートの中は常にできるだけ簡単にする。 平方根のかけ算、割り算は、根号の中どうし、外どうし計算する。 30=6×5なので 6 × 30 = 6×6×5 = 6 5 98=7 2 ×2, 27=3 3 なので 98 = 7 2 27 = 3 3 よって 98 × 27 = 7 2 ×3 3 = 7×3× 2×3 =21 6 6 10 ÷3 2 = 6 3 10 2 = 2 5




平方根の割り算 さわやか さくらぐみ




ルート 根号 の計算方法をマスターしよう スタディクラブ情報局
ルートの中にある数は、2乗すればルートが外れます(<2>参照)。 これを利用して、出来るだけルートの中の数は小さくして答える、という決まりがあります。 例)√50=√2×√5×√5になるので、√50=5√2とします。 √28=√2×√2×√7=2√7 「素因数分解」という技を使えば、素数だけの掛け算に分解できるので、2乗のペアを見つけやすいです(全ての数は ルートの掛け算の基本は、 ルートを1つにして中身だけ計算しちゃう だったよね?? 例題でもおなじさ。 (1) √12 × √32 = 2√3 × 4√2 の平方根部分の掛け算は、 √3 × √2 = √6 になるね! 例の(2)もおなじ。 平方根の掛け算の基本をつかって計算すると、 √7×√21 = √147ルートの計算の解説 ルート同士で四則演算をおこなう場合、足し算・引き算と掛け算・割り算では計算方法が異なります。 ルートの足し算・引き算 ルートの足し算・引き算をおこなう場合は、ルート内の数は同じで




世界一わかりやすい数学問題集中3 2章 平方根




ルート分数の掛け算の計算方法がわかる3ステップ Qikeru 学びを楽しくわかりやすく
ルート 整数掛け算 √9=3でしたが、今回は3=√9のように、整数からルートにする問題をやっていきましょう。この問題の解き方は「二乗してルートをつけるだけ」です。 例えば、4を√で表すとします。平方根の大小関係を不等号で表す問題を解説! 根号を含む式の値の求め方とは? 分母の有理化のやり方はこれでバッチリ! ルートの計算方法まとめ!問題を使って徹底解説! ルートの分数計算、問題解説で完全マスターだ!←今回の記事数値計算の変形例 log 6 2log 6 3 → log 6 6 → 1 対数方程式の変形例 log 2 xlog 2 (x1)=1 → log 2 x (x1)=log 2 2 (例外) 「log 5 18をlog 5 2とlog 5 3で表せ」というような問題では「分ける」方向で変形しますが、高校生が出会う問題の中ではわずかな量です。 ※対数の




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 平方根 のコツ 有理化 加減乗除 展開
ルートの掛け算の問題!やり方は乗法とほとんど同じ!? 中学や高校の数学の計算問題 本日はルートの掛け算の問題をやっていきましょう。ルートの掛け算のやり方は、画像の解説のように、√の ルート分数の掛け算もバッチコイだ。 練習問題:ルート分数の掛け算は有理化をまず先に! 最後に、計算問題をといてみて。 練習問題 つぎの平方根をふくむ計算をしなさい。 7分の√ × √10分の2;2 分配法則を使う平方根の掛け算・割り算 21 乗法公式を使って式の展開をする




数学 中3 21 ルートの計算のまとめ Youtube




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学
ルートの掛け算の問題! やり方は乗法とほとんど同じ! ? 中学3年数学 中学3年数学ルートの掛け算 本日は ルートの掛け算 の問題をやっていきましょう。 ルートの掛け算のやり方は、画像の解説のように、√の中の数同士を掛け算するだけです。となって, x3i=4yi が成り立ちます. *) 要するに, x, y が実数という条件がなければ, x3i=4yi を満たす複素数 x, y は幾らでもあります. 問題3 次の等式を満たす実数 x, y を求めてください. (右の選択肢から選んでください) (1) x4i=5yi 実部の2分の√5 × 5分の√8 × √3分の1 ⇒練習問題の解答はこちら




平方根の割り算 さわやか さくらぐみ
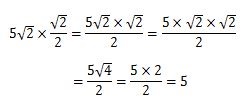



かけざんの問題 平方根の計算 もう一度やり直しの算数 数学
ルートのついた計算は慣れるまでは混乱しやすいものです。 ただちょっとしたコツで簡単になったり難しくなったりしてしまいます。 今回の記事では、分数のルートの計算のコツについて書いてみたいと思います。 ルートの掛け算の計算でルートの中を小さい自然数にすることで、ルート同士の足し算や引き算が可能になるのです。 ルートの簡単化について練習問題を用意したので、ぜひ挑戦してみてください。 時間 00 00 √175 = a√b 175 = a b a = a = 5, b = b = 7 √18 = a√b 18 = a b a = a = 3, b = b = 2 √72 = a√b 72 = a b a = a = 6, b = b = 2 √275 = a√b 275 = a b a = a = 5, b = b = 11 √539 = a√b 539 = a b a = a = 7, b = b = 11基本的に、ルートどうしのかけ算は、ルートの中身をかけ算します。 例2: 2 × 3 × 5 = 30 3つのルートのかけ算も同じく、ルートの中身をかけ算します。 例3: 3 × 6 = 18 = 3 2 かけ算した結果が簡単になる場合は、簡単な形で答えます。 (この例だと、 18 = 3 × 3 × 2 = 3 2 と変形できます) 例4: 2 3 × 4 5 = 8 15 ルートの外側にも数字がある場合、ルートの外側と内側を




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




中学数学 平方根 のコツ 有理化 加減乗除 展開




中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平方根の計算 3分でわかる ルートの掛け算の基本 Qikeru 学びを楽しくわかりやすく
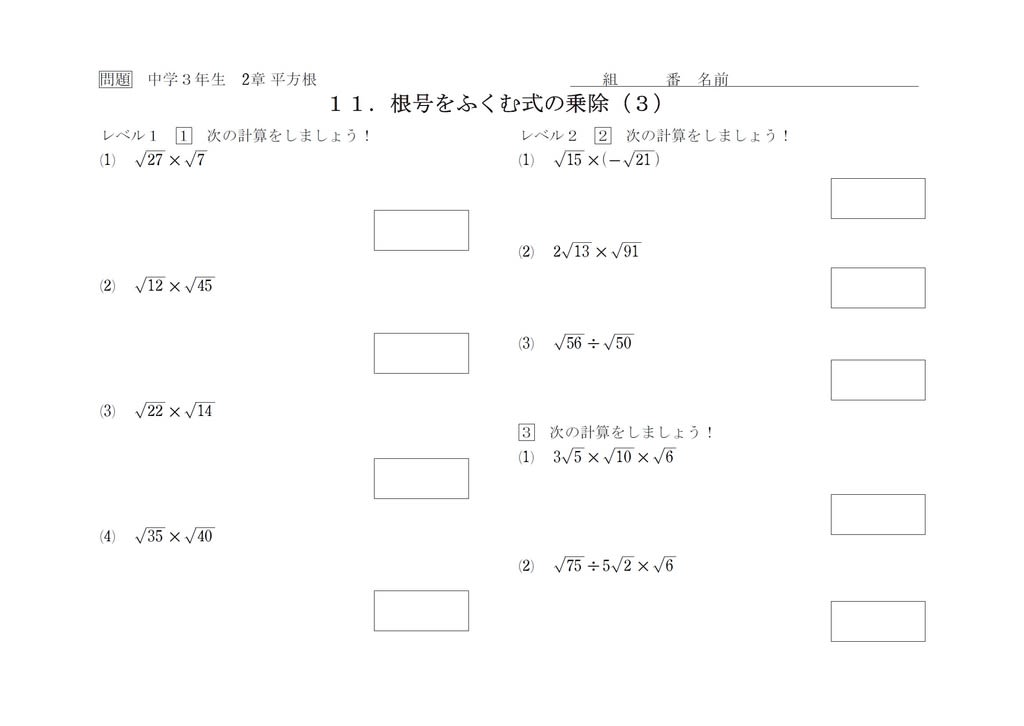



中3 平方根11 乗除3 中学数学の勉強に




平方根の割り算 さわやか さくらぐみ




数学 中3 17 ルートの変形 Youtube




ルートの割り算の問題 やり方は を合体して中で割るだけだ 中学や高校の数学の計算問題
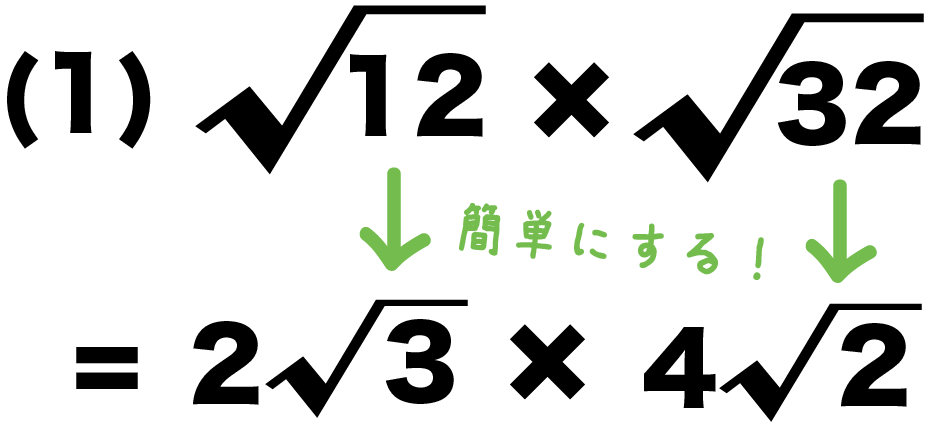



平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




中学3年生 数学 平方根の乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




5秒以内に計算できますか サクッとさばきたいルートの掛け算 暇つぶしに動画で脳トレ




平方根 ルート の重要な計算方法まとめ 数学fun




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




中3 数学 無料学習プリント教材




平方根の計算 3分でわかる ルートの掛け算の基本 Qikeru 学びを楽しくわかりやすく



ルートの掛け算 割り算の計算について教えてください 4 3 Yahoo 知恵袋




平方根 ルート の重要な計算方法まとめ 数学fun



平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




ルートの掛け算のうまいやり方 の中はすぐに計算しない方がいい 中学や高校の数学の計算問題




中3数学 ルートの計算とカッコ カッコの公式 練習編 映像授業のtry It トライイット




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ




平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook




平方根の公式 中学生が覚えるべき掛け算と割り算の公式 中学や高校の数学の計算問題




平方根の掛け算 看護学校の受験数学 中学数学 を分かりやすく図解で説明 Kazアカデミー 大阪の看護学校 看護予備校



平方根の掛け算は 1分でわかる意味 計算のやり方 公式 分数の掛け算




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




ルート の 問題 ニスヌーピー 壁紙




中学3年の数学 動画 ルートのかけ算 わり算の問題 19ch




中3数学 平方根の計算の仕方を極めよう 掛け算 割り算も 都立高校受験応援ブログ



ルートの分数を含む掛け算 割り算がわかりません この画像の計 Yahoo 知恵袋
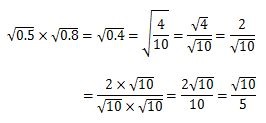



かけざんの問題 平方根の計算 もう一度やり直しの算数 数学




平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




平方根 ルート の重要な計算方法まとめ 数学fun




中3 数学 無料学習プリント教材




平方根 ルート の重要な計算方法まとめ 数学fun




平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師
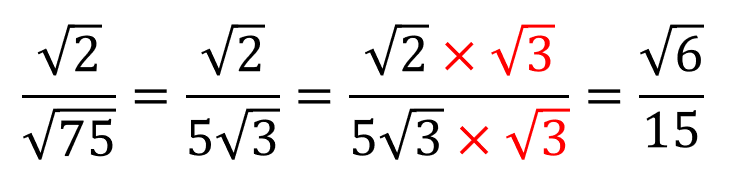



平方根の問題の解き方 6パターン 数学fun




複雑なルートの分数の有理化のやり方と問題 理系ラボ




中学数学 ルート分数の掛け算の2つの練習問題 Qikeru 学びを楽しくわかりやすく




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




世界一わかりやすい数学問題集中3 2章 平方根




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス



平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師




中学3年数学の問題です 整数をルートに入れる問題でよくわからないの 数学 教えて Goo




ルートを簡単にする問題 二乗が作れないやつは を外せない 中学や高校の数学の計算問題




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




平方根の問題の解き方 6パターン 数学fun




中3数学 ルートのかけ算 練習編 映像授業のtry It トライイット
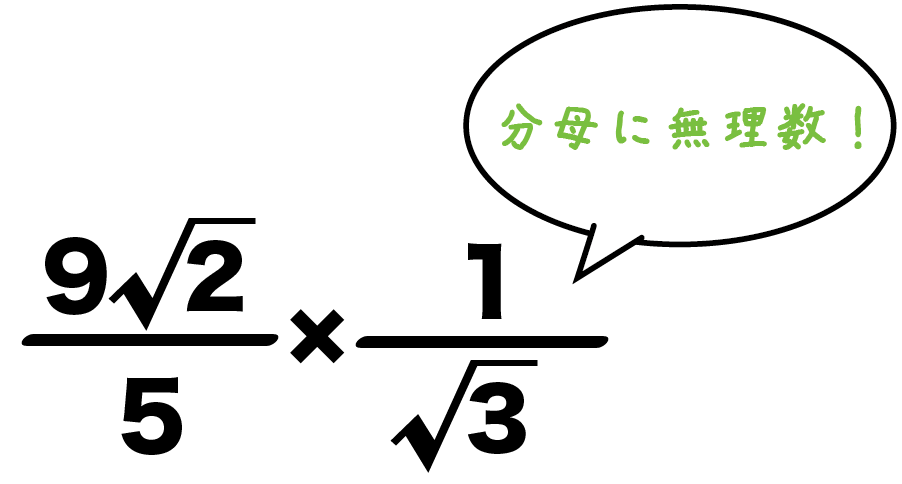



ルート分数の掛け算の計算方法がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




ルートの足し算のやり方 簡単すぎる例題問題を解いてみよう 中学や高校の数学の計算問題




ルートの分数計算 問題解説で完全マスターだ 数スタ




平方根 ルート の重要な計算方法まとめ 数学fun



Studydoctor ルートのかけ算と割り算 中3数学 Studydoctor



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく



1




平方根の掛け算 看護学校の受験数学 中学数学 を分かりやすく図解で説明 Kazアカデミー 大阪の看護学校 看護予備校




中学3年生 数学 平方根の乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




平方根の掛け算 さわやか さくらぐみ




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




中学数学 ルート分数の掛け算の2つの練習問題 Qikeru 学びを楽しくわかりやすく




指数法則を使う問題の計算練習 高校数学の知識庫



1



3




ルートの掛け算のやり方 の中と外を別々に計算しよう 中学や高校の数学の計算問題




中学数学 ルート分数の掛け算の2つの練習問題 Qikeru 学びを楽しくわかりやすく




中学数学3年 いろいろな平方根の計算 平方根と式の値 受験の月




整数をルートにする方法 5秒で計算できる簡単な問題だ 中学や高校の数学の計算問題
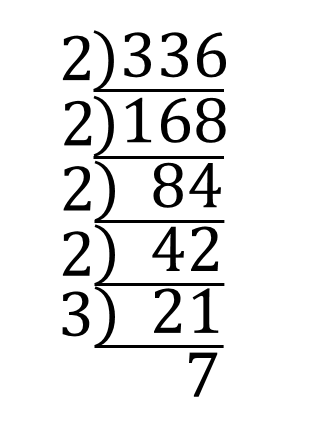



平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ
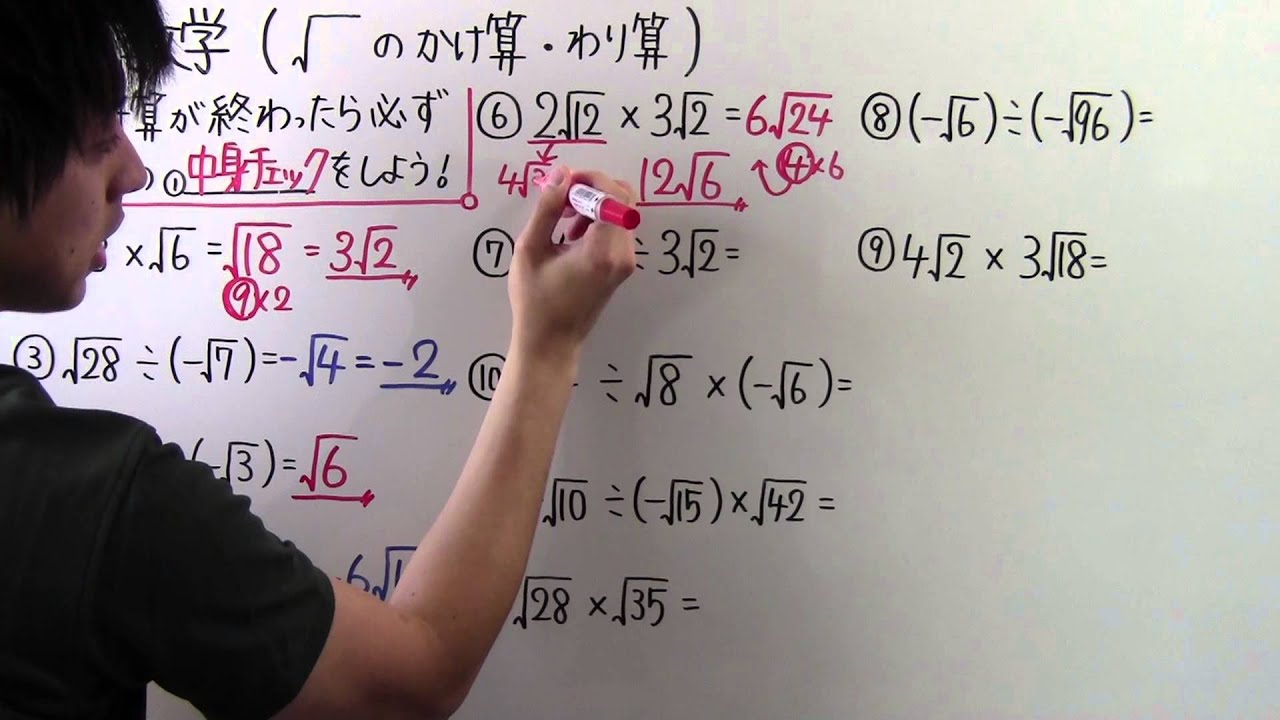



数学 中3 18 ルートのかけ算 わり算 Youtube



分数 整数 ルートの計算方法を教えてください下の画像の計算方法を教えて Yahoo 知恵袋



1




平方根 ルート の重要な計算方法まとめ 数学fun
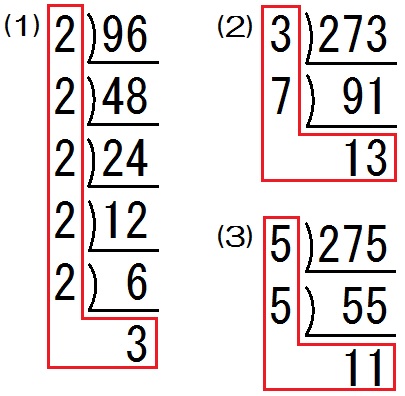



中学数学 平方根 のコツ 素因数分解 ルートを簡単にする計算
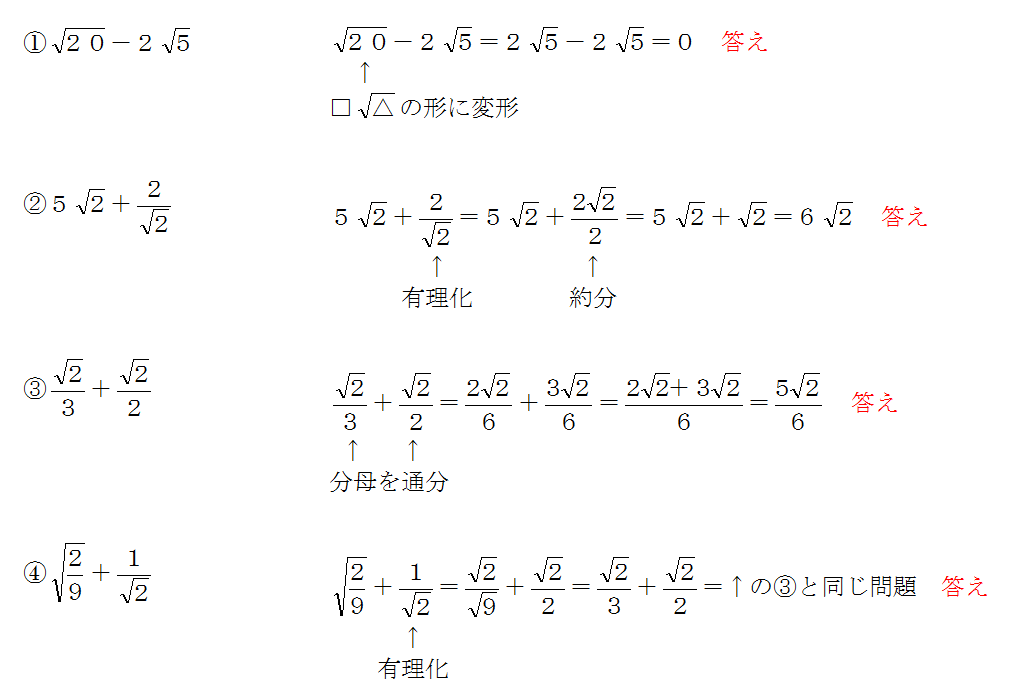



平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師




中学3年生 数学 平方根の乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



平方根の掛け算は 1分でわかる意味 計算のやり方 公式 分数の掛け算
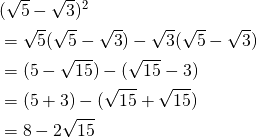



ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




平方根の掛け算 さわやか さくらぐみ




平方根 ルート の重要な計算方法まとめ 数学fun




中3数学 ルートの計算とカッコ カッコの公式 練習編 映像授業のtry It トライイット
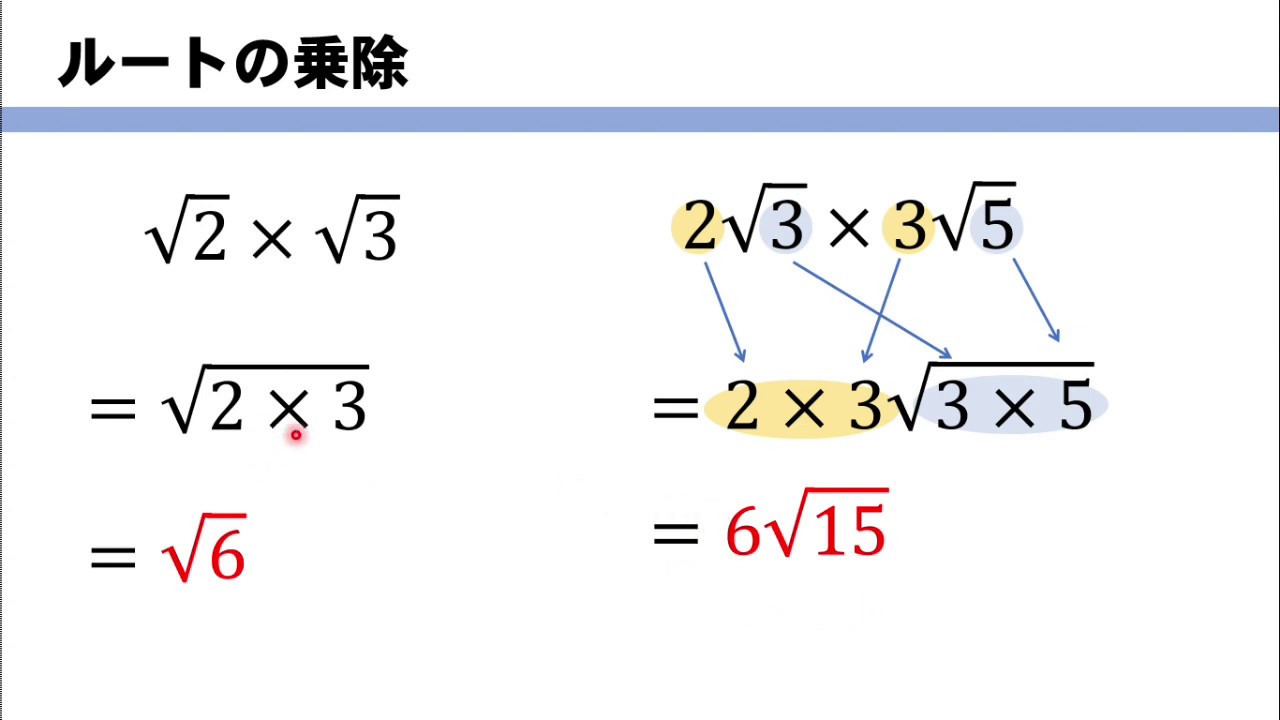



平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




平方根 ルート の重要な計算方法まとめ 数学fun




愛されし者 ルート 計算 足し算



0 件のコメント:
コメントを投稿